Below, you see some reciprocal lattice points that are labeled with $h$, $k$, and $l$. A green reciprocal lattice vector stretches from the origin to one of the reciprocal lattice points.

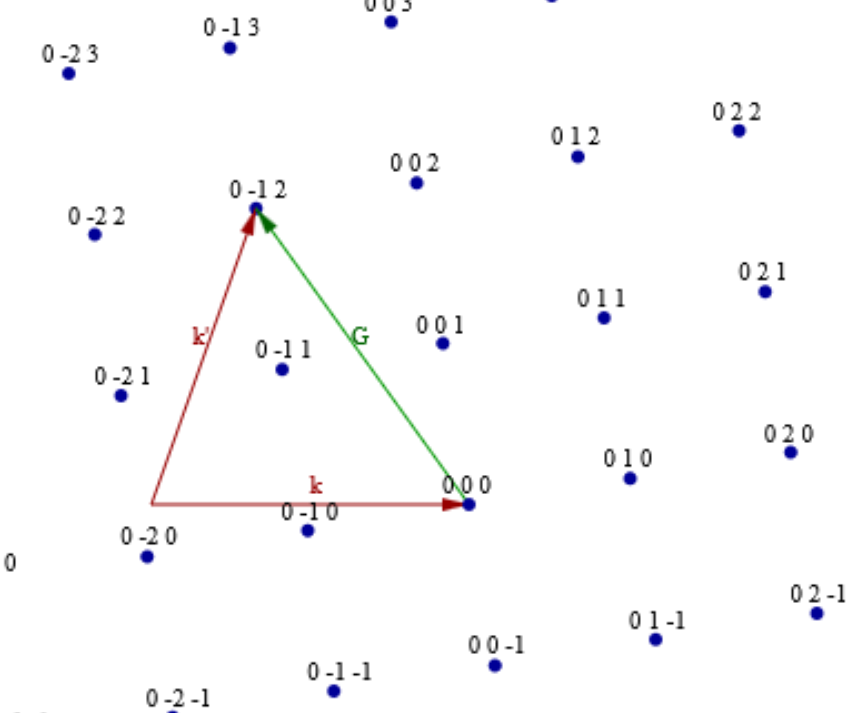
The diffraction condition $\Delta\vec{k}=\vec{G}$, will be satisfied if we hold the tails of the wave vectors $\vec{k}$ and $\vec{k}'$ together and can put the head of vector $\vec{k}$ at the origin while the head of vector $\vec{k}'$ is at $\vec{G}$. If the tails of both $k$-vectors have to be held together and the head of the $\vec{k}$ is at the origin, the $\vec{G}$ vector must be within a sphere of radius $2|\vec{k}|$ for the diffraction condition to be valid. There will only be a finite number of reciprocal lattice vectors that satisfy the diffraction condition. This number can be estimated by dividing the volume of the sphere $4\pi(2|\vec{k}|)^3/3$ by the volume per reciprocal lattice point $\vec{b}_1\cdot (\vec{b}_2\times \vec{b}_3)$. There are typically hundreds or thousands of reciprocal lattice vectors that can be measured. The number can be increased by choosing a shorter wavelength for the x-rays.

The diffraction condition can be visualized with an Ewald construction as illustrated below. The incoming wavevector $\vec{k}$ is drawn so that it ends at the origin of reciprocal space. In an experiment, $\vec{k}$ is typically held constant because the x-ray source is heavy. A sphere is drawn around the tail of the $\vec{k}$ vector with a radius $|\vec{k}|$. Whenever a reciprocal lattice point lies on the sphere, the diffraction condition will be satisfied. In the simulation below, the crystal is aligned so that the $(hkl)$ plane is parallel to the beam. The crystal is then rotated around the normal to the $(hkl)$ plane. Since $\vec{G}_{hkl}$ is normal to the $(hkl)$ plane, the reciprocal lattice points are rotated around $\vec{G}_{hkl}$. Every time the crystal is rotated a little, the detector is scanned around the $(hkl)$ plane to search for diffraction peaks. When diffraction occurs, both $\vec{k}$ and $\vec{k}'$ will lie on the Ewald sphere. The angle between $\vec{k}$ and $\vec{k}'$ is $2\theta$. Press the and buttons to rotate the crystal.

Primitive lattice vectors:  $\vec{a}_1=$ $\hat{x}+$ $\hat{y}+$ $\hat{z}$ [Å]   $\vec{a}_2=$ $\hat{x}+$ $\hat{y}+$ $\hat{z}$ [Å]  $\vec{a}_3=$ $\hat{x}+$ $\hat{y}+$ $\hat{z}$ [Å]  The x-rays scan the $hkl$ plane. $h=$ $k=$ $l=$  X-ray wavelength λ = [Å] = 1.540598 Å = 2.28975 Å = 0.7093165 Å

Reciprocal lattice points in the in the ( ) plane
Your browser does not support the canvas element.	Primitive reciprocal lattice vectors $\vec{b}_1=$ [ , , ] [Å-1] $\vec{b}_2=$ [ , , ] [Å-1] $\vec{b}_3=$ [ , , ] [Å-1] $\phi$ The approximate number of reciprocal lattice points where diffraction can be observed can be obtained by dividing the volume of a sphere of radius $2|\vec{k}|$ by the volume of a primitive unit cell in reciprocal space. This approximate number is .