PHY.K02UF Molecular and Solid State Physics
|
| ||||
PHY.K02UF Molecular and Solid State Physics | ||||
A crystal consists of a pattern of atoms (the basis) that is repeated periodically. A consequence of this periodicity is that the electron density in a crystal is a periodic function. Calculating the electron density is central to our understanding of solids and will be a major topic of this book. To describe the electron density mathematically, it will be necessary to generalize the concept of a Fourier series to two-dimensional and three-dimensional periodic functions. This chapter starts with a review of a Fourier series in one dimension and then extends this concept to two and three dimensions.
For a one-dimensional function $f(x)$ with periodicity $a$, a Fourier series can be written in terms of sines and cosines,
$$f(x)= c_0 +\sum\limits_{n=1}^{\infty}\left(c_n\cos(2\pi nx/a) + s_n\sin(2\pi nx/a)\right).$$Here $c_n$ and $s_n$ are constants. The periodic function is a constant $c_0$ plus sinusoidal functions with wavelengths $a/n$. The terms with $n=1$ are called the fundamental components, and the terms with $n > 1$ are the harmonics. If the function $f(x)$ is known, the constants can be calculated with the formulas,
$$c_n = \frac{2}{a}\int\limits_{0}^af(x)\cos(2\pi nx/a)dx,$$ $$s_n = \frac{2}{a}\int\limits_{0}^af(x)\sin(2\pi nx/a)dx.$$These formulas can be seen as the projection of $f(x)$ onto $\cos(2\pi nx/a)$ and $\sin(2\pi nx/a)$. If $f(x)$ is a square wave function,
| $\frac{f(x)}{f_0}$ | |
$x$ |
the coefficients are $c_n = \frac{2}{\pi n}\sin\left(\frac{\pi n}{2}\right)$, $s_n=0$. The form below will show you the waveform when the Fourier series is truncated at $n_{\text{max}}$.
Even for $n_{\text{max}}=100$, there is a small deviation of the Fourier series from the ideal square wave. The sharp corners of the square wave require very short wavelengths to model accurately.
There are buttons in the panel below that display various periodic functions using all terms up to $n=11$. The upper panel shows the function, and the lower panel shows the Fourier components that make up the function. Typically, the amplitude of the Fourier components decreases as the wavelengths get shorter. An interesting exception is the comb function, where the coefficients of all of the Fourier components are the same.
To make the generalization of a Fourier series to two and three dimensions, it is convenient to express the sine and cosine terms as complex exponentials, $\sin(x) = (e^{ix}-e^{-ix})/(2i)$ and $\cos(x) = (e^{ix}+e^{-ix})/2$. The Fourier series can then be written compactly as,
$$f(x) = \sum\limits_{n=-\infty}^{\infty}f_{n}e^{iG_nx},\qquad G_n = \frac{2\pi n}{a}, \qquad f_{n} = \frac{c_n}{2} - i\frac{s_n}{2}.$$The real part of the Fourier coefficients $f_n$ encodes the cosine components and the imaginary part of the Fourier coefficients encodes the sine components. At first, this seems more complicated because we have replaced friendly functions like $\sin(x)$ and $\cos(x)$ with complex exponentials. However, this is a mathematically convenient form because exponential functions are easy to integrate and differentiate. They can also be easily multiplied together by adding the exponents. To plot the series, we can convert back to sines and cosines using Euler's formula, $e^{ix}= \cos(x)+i\sin(x).$
A review of the exponential function
The form below allows you to compose a real periodic function from its Fourier components. The period of the function is $a=1$.
| $f(x)$ | |
$x$ |
Experiment with the sliders to create different periodic functions. If you press 'zero' and then only move the sliders for the real parts, the function will be even, and if you press 'zero' and then only move the sliders for the imaginary parts, the function will be odd. If both real and imaginary parts are nonzero, the function will be periodic, but it won't have an odd or even symmetry.
The Fourier coefficients in this example have been restricted to the case where $f_{-n}=f_{n}^*$ so that the resulting function will be real. If $f_n = \frac{c_n}{2} - i\frac{s_n}{2}$, then $f_{-n} = \frac{c_n}{2} + i\frac{s_n}{2}$, and there will be two terms in the sum where the imaginary parts cancel out,
$$f_n\exp\left(i\frac{2\pi nx}{a}\right) + f_{-n}\exp\left(i\frac{-2\pi nx}{a}\right)\\ =\left(\frac{c_n}{2} - i\frac{s_n}{2}\right)\left(\cos\left(\frac{2\pi nx}{a}\right)+i\sin\left(\frac{2\pi nx}{a}\right)\right) + \left(\frac{c_n}{2} + i\frac{s_n}{2}\right)\left(\cos\left(\frac{2\pi nx}{a}\right)-i\sin\left(\frac{2\pi nx}{a}\right)\right)\\ =c_n\cos\left(\frac{2\pi nx}{a}\right) + s_n\sin\left(\frac{2\pi nx}{a}\right).$$Therefore, the function is real if $f_{-n}=f_{n}^*$.
Now consider three-dimensional periodic functions like the electron density of a crystal. This can be thought of as a function that is defined in the primitive unit cell and then repeated on the Bravais lattice. We seek a function that can be written as a Fourier series. The generalization of a Fourier series to higher dimensions is,
$$f(\vec{r})=\sum \limits_{\vec{G}} f_{\vec{G}}\exp \left(i\vec{G}\cdot\vec{r}\right).$$Here $\vec{G}$ are the reciprocal lattice vectors, which we still need to determine, and $f_{\vec{G}}$ are the Fourier coefficients that can be complex numbers. One term in this sum has the form,
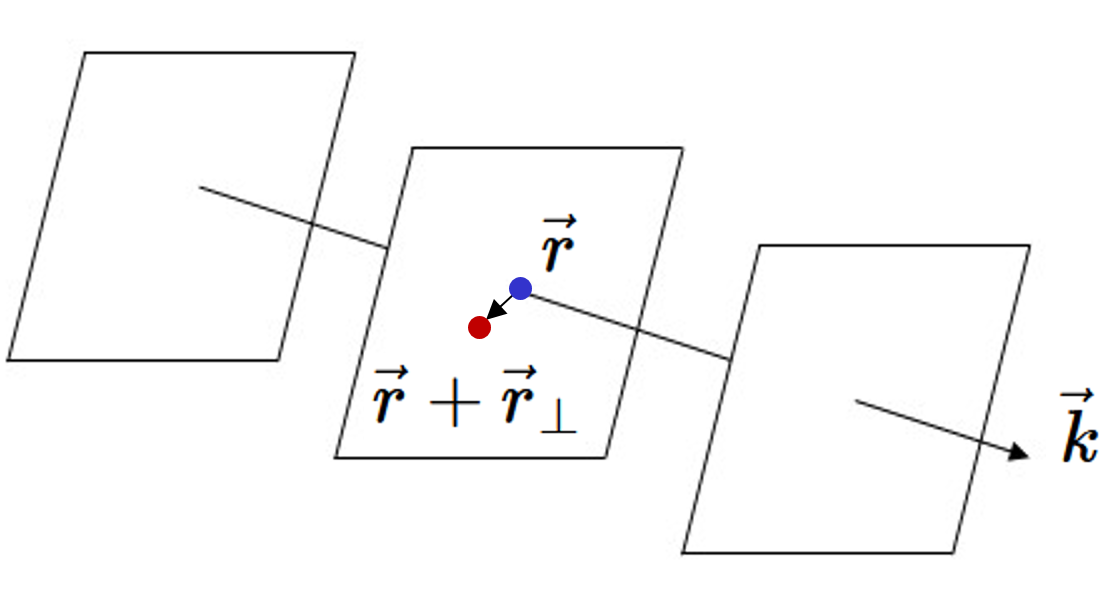
$$\exp \left(i\vec{G}\cdot\vec{r}\right)= \exp \left(i(G_xx+ G_yy + G_zz)\right) = \exp \left(i(G_xx)\right)\exp \left(i(G_yy)\right)\exp \left(i(G_zz)\right) \\ = \left(\cos(G_xx) + i\sin(G_xx)\right) \left(\cos(G_yy) + i\sin(G_yy)\right) \left(\cos(G_zz) + i\sin(G_zz)\right).$$The final form makes it clear that this is a periodic function. A product of sine and cosine functions will always produce a periodic function. The wavelength of the function in the $x-$direction is set by $G_x$, the wavelength of the function in the $y-$direction is set by $G_y$, and the wavelength of the function in the $z-$direction is set by $G_z$. The function $\exp(i\vec{G}\cdot\vec{r})$ is called a plane wave. Plane waves are commonly written with a wave vector $\vec{k}$, $\exp(i\vec{k}\cdot\vec{r})$. The direction that the wave is travelling is given by the direction of $\vec{k}$ and the wavelength of the wave is $\lambda = 2\pi/|\vec{k}|$. Consider the value of the plane wave at the blue point $\vec{r}$ in the figure below. In general, the value at this point is some complex number. Now move away from that point in a direction perpendicular to $\vec{k}$ to the red point $\vec{r}+\vec{r}_{\perp}$. The value of the plane wave at every point on the plane that passes through $\vec{r}$ and is perpendicular to $\vec{k}$ has the same value, $e^{i\vec{k}\cdot\left(\vec{r} +\vec{r}_{\perp}\right)} = e^{i\vec{k}\cdot\vec{r}}$. The function $\exp(i\vec{k}\cdot\vec{r})$ is called a plane wave because its value is constant on every plane perpendicular to $\vec{k}$.
Below is a plot of the real part of a plane wave. By choosing different values for $\vec{k}$, the direction of the plane wave changes, and the wavelength changes.
$\vec{k}=6\,\hat{x}$ | $\vec{k}=6\,\hat{y}$ | $\vec{k}=4\,\hat{x}+4\,\hat{y}$ | $\vec{k}=3\,\hat{x}-5\,\hat{y}$ |
Reciprocal space is a space of plane waves. Every point in a reciprocal space spanned by the vectors $\vec{k}=k_x\hat{x}+k_y\hat{y} +k_z\hat{z}$ corresponds to a plane wave. The direction of the $k$-vector indicates the direction the plane wave is moving, and $2\pi/|\vec{k}|$ is the wavelength of the plane wave. A distance $|\vec{k}|$ measured in reciprocal space is measured in units of 1/meters and this is why the space is reciprocal. While $\vec{k}$ varies continuously in reciprocal space, the reciprocal lattice vectors $\vec{G}$ that we need for a Fourier series are discrete points in reciprocal space.
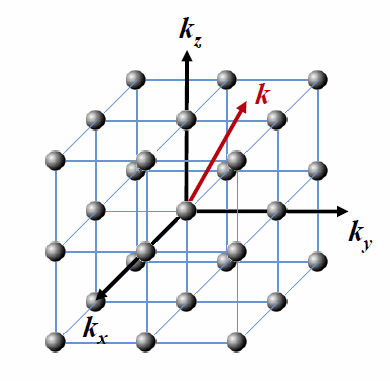
The red vector is a $k$-vector in reciprocal space. The black points represent a reciprocal lattice.
A three-dimensional periodic function has to have the same value if it is translated by any of the primitive lattice vectors. This requires that the function at $\vec{r} = 0$, $\vec{r} = \vec{a}_1$, $\vec{r} = \vec{a}_2$, and $\vec{r} = \vec{a}_3$ all have the same value. At $\vec{r}=0$, $\exp\left(i\vec{G}\cdot\vec{r}\right) = 1$ so we have the periodicity conditions on $\vec{G}$ that,
$$ \exp\left(i\vec{G}\cdot\vec{a}_1\right) = 1, \\ \exp\left(i\vec{G}\cdot\vec{a}_2\right) = 1, \\ \exp\left(i\vec{G}\cdot\vec{a}_3\right) = 1.$$These conditions will be satisfied if
$$ \vec{G}\cdot\vec{a}_1 = 2\pi h, \\ \vec{G}\cdot\vec{a}_2 = 2\pi k, \\ \vec{G}\cdot\vec{a}_3 = 2\pi l,$$where $h$, $k$, and $l$ are positive or negative integers. The case of $h=1$ corresponds to the periodic function having one wavelength between $\vec{r} = 0$ and $\vec{r} = \vec{a}_1$, the case of $h=2$ corresponds to the periodic function having two wavelengths between $\vec{r} = 0$ and $\vec{r} = \vec{a}_1$, etc.
The periodicity conditions will be satisfied if $\vec{G}$ has the form,
$$\vec{G}_{hkl} = h\vec{b}_1 + k\vec{b}_2 + l\vec{b}_3,$$Where the vectors $\vec{b}_j$ are called the primitive reciprocal lattice vectors and they are defined by the relation,
$$\vec{a}_i\cdot\vec{b}_j = 2\pi\delta_{ij}.$$Here $\delta_{ij}$ is the Kronecker delta,
$$\delta_{ij}= \begin{cases} 1 & \mbox{for } i=j \\ 0, & \mbox{for } i\ne j \end{cases}.$$Since $i$ and $j$ can each be $x$, $y$, or $z$, the relation $\vec{a}_i\cdot\vec{b}_j = 2\pi\delta_{ij}$, is really nine equations for the nine unknowns $b_{1x}$, $b_{1y}$, $b_{1z}$, $b_{2x}$, $b_{2y}$, $b_{2z}$, $b_{3x}$, $b_{3y}$, $b_{3z}$. Once we solve these equations for the primitive reciprocal lattice $\vec{b}_{1}$, $\vec{b}_{2}$, and $\vec{b}_{3}$, we can construct the reciprocal lattice vectors that will have the correct periodicity in three dimensions, $\vec{G}_{hkl} = h\vec{b}_1 + k\vec{b}_2 + l\vec{b}_3$. We can check this by inserting $\vec{G}_{hkl}$ into the periodicity conditions,
$$ \vec{G}_{hkl}\cdot\vec{a}_1 =h\vec{b}_1\cdot\vec{a}_1 = 2\pi h, \\ \vec{G}_{hkl}\cdot\vec{a}_2 =k\vec{b}_2\cdot\vec{a}_2 = 2\pi k, \\ \vec{G}_{hkl}\cdot\vec{a}_3 =l\vec{b}_3\cdot\vec{a}_3 = 2\pi l.$$Finally, we can write a Fourier series in three dimensions as,
$$f(\vec{r})=\sum \limits_{hkl} f_{\vec{G}_{hkl}}\exp \left(i\vec{G}_{hkl}\cdot\vec{r}\right).$$Mostly, we will be interested in real periodic functions. The condition that the function be real is $f_{-\vec{G}}=f_{\vec{G}}^*$.
If we consider the points where the reciprocal lattice vectors $\vec{G}_{hkl} = h\vec{b}_1 + k\vec{b}_2 + l\vec{b}_3$ end, they form an infinite periodic lattice of points like a Bravais lattice. Notice that the reciprocal lattice vectors only depend on the primitive lattice vectors in real space, and not any other properties of the periodic function. This means that a Bravais lattice in real space can be associated with another infinite periodic lattice of points where the reciprocal lattice vectors end. This is called the reciprocal lattice of a Bravais lattice. To calculate a reciprocal lattice, it is convenient to introduce another way to calculate the primitive reciprocal lattice vectors.
\begin{eqnarray} \vec{b}_1=2\pi \frac{\vec{a}_2\times\vec{a}_3}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}&\hspace{2cm}&\vec{a}_1=2\pi \frac{\vec{b}_2\times\vec{b}_3}{\vec{b}_1\cdot\left(\vec{b}_2\times\vec{b}_3\right)} \\ \vec{b}_2=2\pi \frac{\vec{a}_3\times\vec{a}_1}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}&\hspace{2cm}&\vec{a}_1=2\pi \frac{\vec{b}_3\times\vec{b}_1}{\vec{b}_1\cdot\left(\vec{b}_2\times\vec{b}_3\right)} \\ \vec{b}_3=2\pi \frac{\vec{a}_1\times\vec{a}_2}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}&\hspace{2cm}&\vec{a}_3=2\pi \frac{\vec{b}_1\times\vec{b}_2}{\vec{b}_1\cdot\left(\vec{b}_2\times\vec{b}_3\right)} \end{eqnarray}Because of the cross product, $\vec{b}_1$ is perpendicular to $\vec{a}_2$ and $\vec{a}_3$ so $\vec{a}_2\cdot\vec{b}_1 = \vec{a}_3\cdot\vec{b}_1=0$ and $\vec{a}_1\cdot\vec{b}_1= 2\pi \vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)/\left( \vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)\right) = 2\pi$ so that the expressions with the cross products are the same as $a_ib_j=2\pi\delta_{ij}$.
By applying these rules, one can show that a simple cubic lattice has a simple cubic reciprocal lattice.
$$\text{sc:}\qquad\vec{a}_1=a\hat{x},\quad \vec{a}_2=a\hat{y},\quad\vec{a}_3=a\hat{z},\\ \vec{b}_1=\frac{2\pi}{a}\hat{k}_x,\quad \vec{b}_2=\frac{2\pi}{a}\hat{k}_y,\quad\vec{b}_3=\frac{2\pi}{a}\hat{k}_z.$$An fcc lattice has a bcc reciprocal lattice.
$$\text{fcc:}\qquad\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{z}),\quad \vec{a}_2=\frac{a}{2}(\hat{x}+\hat{y}),\quad\vec{a}_3=\frac{a}{2}(\hat{y}+\hat{z}),\\ \vec{b}_1=\frac{2\pi}{a}(\hat{k}_x-\hat{k}_y+\hat{k}_z),\quad \vec{b}_2=\frac{2\pi}{a}(\hat{k}_x+\hat{k}_y-\hat{k}_z),\quad\vec{b}_3=\frac{2\pi}{a}(-\hat{k}_x+\hat{k}_y+\hat{k}_z).$$A bcc lattice has an fcc reciprocal lattice.
$$\text{bcc:}\qquad\vec{a}_1=\frac{a}{2}(\hat{x}+\hat{y}-\hat{z}),\quad \vec{a}_2=\frac{a}{2}(-\hat{x}+\hat{y}+\hat{z}),\quad\vec{a}_3=\frac{a}{2}(\hat{x}-\hat{y}+\hat{z}),\\ \vec{b}_1=\frac{2\pi}{a}(\hat{k}_x+\hat{k}_y),\quad \vec{b}_2=\frac{2\pi}{a}(\hat{k}_y+\hat{k}_z),\quad\vec{b}_3=\frac{2\pi}{a}(\hat{k}_x+\hat{k}_z).$$A hexagonal lattice has a hexagonal reciprocal lattice.
$$\text{hex:}\qquad\vec{a}_1=a\hat{x},\qquad\vec{a}_2=\frac{a}{2}\hat{x}+\frac{\sqrt{3}a}{2}\hat{y},\qquad\vec{a}_3=c\hat{z},\\\vec{b}_1=\frac{2\pi}{\sqrt{3}a}\left(\sqrt{3}\hat{k}_x-\hat{k}_y\right),\qquad\vec{b}_2=\frac{4\pi}{\sqrt{3}a}\hat{k}_y,\qquad\vec{b}_3=\frac{2\pi}{c}\hat{k}_z.$$The form below will calculate the primitive reciprocal lattice vectors given the real-space primitive lattice vectors.
Primitive reciprocal lattice vectors
| $\vec{b}_1=2\pi\frac{\vec{a}_2\times\vec{a}_3}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}=$ $\hat{k}_x+$ $\hat{k}_y+$ $\hat{k}_z$ [m-1] |
| $\vec{b}_2=2\pi\frac{\vec{a}_3\times\vec{a}_1}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}=$ $\hat{k}_x+$ $\hat{k}_y+$ $\hat{k}_z$ [m-1] |
| $\vec{b}_3=2\pi\frac{\vec{a}_1\times\vec{a}_2}{\vec{a}_1\cdot\left(\vec{a}_2\times\vec{a}_3\right)}=$ $\hat{k}_x+$ $\hat{k}_y+$ $\hat{k}_z$ [m-1] |
Below are some links to calculations of the Fourier coefficients $f_{\vec{G}}$ for periodic functions in two dimensions and three dimensions. What is remarkable about these calculations is that they are valid for all Bravais lattices. For instance, if cubes with sides of length $a$ are repeated on a three-dimensional Bravais lattice, the Fourier series for a function $f(\vec{r})$ that has a value $C$ inside the cubes and 0 outside the cubes is,
$$f(\vec{r})=\sum\limits_{\vec{G}}\frac{16C\sin\left(\frac{G_xa}{4}\right)\sin\left(\frac{G_ya}{4}\right)\sin\left(\frac{G_za}{4}\right)}{a^3G_xG_yG_z}\exp\left(i\vec{G}\cdot\vec{r}\right),$$independent of which Bravais lattice it is. Here $\vec{G}$ are the reciprocal lattice vectors of that Bravais lattice.