In an experiment, the wavelength of the x-rays is typically held constant so the the length of the incoming $\vec{k}$-vector is held fixed. Consider what will happen if we allow $|\vec{k}|$ to take on any value. The diffraction condition is,

$$\vec{k}'-\vec{k} = \vec{G},$$

which can be drawn a $\vec{k}'+(-\vec{k})=\vec{G}$.

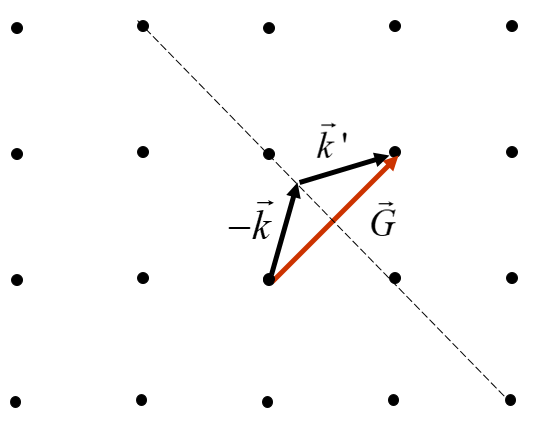
An equilateral triangle is formed since $|\vec{k}|=|\vec{k}'|$. If we change the length of $|\vec{k}|$, the vector $-\vec{k}$ will always end on a plane perpendicular to $\vec{G}$ that cuts the vector $\vec{G}$ in half (indicated by the dashed line). This plane is known as a Brillouin zone boundary. All reciprocal lattices have inversion symmetry, so if there is diffraction at $\vec{k}$, there is also diffraction at $-\vec{k}$. This allows us to make the following statement about the Brillouin zone boundary:

The diffraction condition will be satisfied if $\vec{k}$ falls on a Brillouin zone boundary.

More Brillouin zone boundaries can be drawn by biscecting other reciprocal lattice vectors with their normal planes.

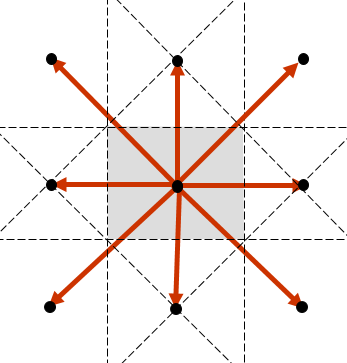
The (gray) region of reciprocal space that can be reached from the origin without crossing any Brillouin zone boundaries is called the first Brillouin zone. The first Brillouin zone is the Wigner-Seitz cell in reciprocal space and contains all of the long-wavelength waves. The wavelength diverges as $|\vec{k}| \rightarrow 0$, and the shortest wavelengths near the boundary are about twice as long as a primitive lattice vector. All of the $\vec{k}$-vectors within the first Brillouin zone cannot cause diffraction because $|\vec{k}|+ |\vec{k}'| = 2|\vec{k}| < |\vec{G}|$. The second Brillouin zone is the region of $\vec{k}$-space that can be reached from the origin by passing one Brillouin zone boundary, and the $n$th Brillouin zone is the region of $\vec{k}$-space that can be reached from the origin by crossing $n-1$ Brillouin zone boundaries.

Drawing Brillouin zones in 2D.

Drawing Brillouin zones in 3D.

It will sometimes be important to specify which way waves are moving through a crystal. Waves with a certain wavelength may diffract when moving in one direction but not when moving in another direction. For every Bravais lattice, there are directions that are related by symmetry. For instance, for cubic crystals, waves that diffract in the $x$-direction will also diffract in the $y$- and $z$-driections. The symmetric directions for the different Bravais lattices have been given names to make it easier to discuss waves travelling in different directions for different crystal structures. There are links below to rotatable drawings of the first Brillouin zones displaying the symmetry points.

Triclinic a ≠ b ≠ c α ≠ β ≠ γ	Triclinic
Monoclinic a ≠ b ≠ c α ≠ 90° β = γ= 90°	Monoclinic simple	Monoclinic Base centered
Orthorhombic a ≠ b ≠ c α = β = γ = 90°	Orthorhombic simple	Base centered
	Face centered	Body centered
Tetragonal a = b ≠ c α = β = γ = 90°	Simple	Body centered
Trigonal a = b = c α = β = γ ≠ 90°	Trigonal = Rhombohedral
Hexagonal a = b ≠ c α = 120°, β = γ = 90°	Hexagonal
Cubic a = b = c α = β = γ = 90°	Simple Cubic	Face Centered Cubic	Body Centered Cubic